Menu

Plug Flow Reactors (PFR) : mass balance expression

Follow us on Twitter 
Question, remark ? Contact us at contact@myengineeringtools.com

1. Plug Flow Reactors
2. Plug Flow reactor in steady state : mass balance
3. Plug flow reactor : no volumetric flow variation

Plug flow reactors (PFR) are a very specific type of reactor, different from agitated vessels for example. Instead of having the fluids in relatively large tank, the fluid is pushed in a reactor having a cylindrical shape which can be as simple as a pipe.This page focusing in applying the general mass balance equations to PFR reactors.

1. Plug Flow Reactors

A Plug Flow Reactor is a continuous reactor equipped with an inlet of reactants and an outlet of the content of the reactor which are done continuously during the operation of the reactor.

Plug flow reactor principle

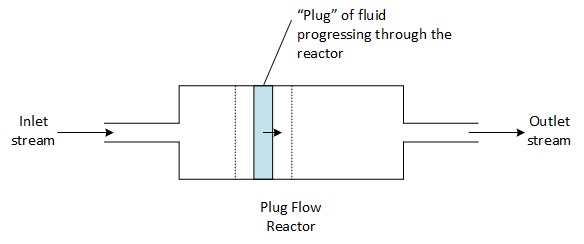
A plug flow reactor has no agitator, it has a cylindrical shape which allows the fluid to progress with a minimal amount of back mixing, as a consequence all the particles of fluid that enter the PFR have the same residence time. The plug flow reactor can indeed be considered as a succession of thin  slices of fluid, constituting a small batch reactor, perfectly stirred within the slice, which moves ahead in the reactor as piston.

The general mass balance equation can then be expressed the following way for one of the slices of fluids in the reactor :

Inlet = Outlet + Consumption + Accumulation

The units of each component of the expression is a material flowrate : mol/s for instance.

2. Plug Flow reactor in steady state : mass balance

The study is done on a small slice of the reactor, of volume dV. This small slice of fluid behaves like a small CSTR reactor : it is very small and thus assumed perfectly agitated, and it is in steady state. The mass balance for the volume dV can then be done, using the general mass balance equation :

FA,i = FA,o + r'A.dV + dnA/dt

With :

FA,i : the molar flow at the inlet of the slice dV
FA,o : the molar flow at the outlet of the slide dV

Top 5 Most Popular 
1. Compressor Power Calculation
2. Pump Power Calculation
3. Pipe Pressure Drop Calculation
4. Fluid Velocity in pipes
5. Churchill Correlation (friction factor)

As the small reactor of volume dV is in steady state, we can assume that : dnA/dt = dnB/dt = dnC/dt = dnD / dt = 0

FA,i = FA,o + r'A.dV

It is possible to express FA,o = FA,i + (dFA,i/dV).dV as the flow of reactant A is expected to vary just a little bit from the inlet flow in the volume dV.

FA,i = FA,i + (dFA,i/dV).dV + r'A.dV

It allows to calculate the general expression of the reaction of consumption of the reactant A in a plug flow reactor as :

r'A = - (dFA,i/dV)

Considering the reaction A + B = C + D, the other reaction speed can be expressed, for a slice of volume dV in the piston reactor, as :

r'B = - (dFB,i/dV)
rC = (dFC,i/dV)
rD = (dFD,i/dV)


3. Plug flow reactor : no volumetric flow variation

In case the volumetric flow within the reactor stays constant (Qi = Qo = Q at any point in the reactor), the reaction speeds above can be simplified and expressed as a function of the concentration.

FA,i = Q.[A]i

r'A = - (dFA,i/dV) = -Q.(d[A]i/dV)

In this expression, the ratio dV/Q can be identified : it is the time required by the particles to go through the small volume dV, integrated over the whole reactor, it gives τ the residence of the particles in the plug flow reactor, thus dV/Q is dτ.

The reaction speed can then be expressed as :

r'A = -(d[A]i/dτ)

3. Case of a reaction with known stoechiometry

In case the reaction stoechiometry is know, the reaction speed above can just be written by adding the stoechiometry coefficient νA.

rA = (1/νA)*(d[A]i/dτ)

d[A]i/dτ = νA * rA

The stoechiometric coefficient is positive for a product of the reaction and negative for a reactant that is consumed.